Worked example estimating the post-test probability of breast cancer
The examples below illustrate the difference in post-test probability of breast cancer following a mammogram in a female with no risk factors (Estimating post-test probability of breast cancer: female with no risk factors but a positive mammogram result) and a female with a breast lump (Estimating post-test probability of breast cancer: female with a breast lump and a positive mammogram result). Assume the prevalence of breast cancer in 40-year-old females is approximately 0.1%, and that a mammogram has a specificity of 95% and a sensitivity of approximately 97%.
With a specificity of 95%, a mammogram will have around 5% false positive findings. The 97% sensitivity means mammography will correctly identify around 97% of those with breast cancer and miss 3% (false negatives).
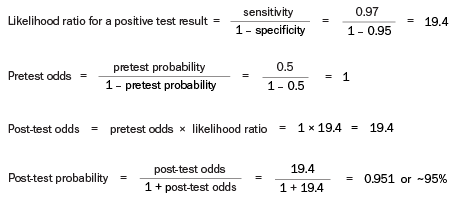
Can you estimate the post-test probability of breast cancer in a 40-year-old female who has no particular risk factors for breast cancer in her history and who has a normal breast examination, but a positive mammogram result?
This female has no other risk factors for breast cancer, so the pretest probability is the same as the prevalence in females of this age in the general population (0.1%). Approximately 1 out of 1000 females will have breast cancer, and approximately 50 females in this group of 1000 will have a false positive mammogram result. The calculated post-test probability of breast cancer in this female with a positive mammogram result is approximately 2% (see calculation below).
Calculation:
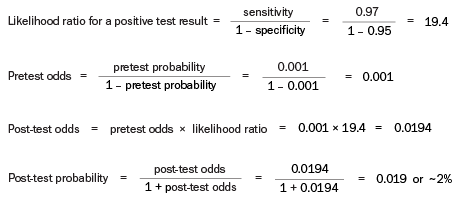
Can you estimate the post-test probability of breast cancer in a 40-year-old female who has a breast lump and a positive mammogram result?
When the clinical findings suggest a higher pretest probability of breast cancer, the post-test probability is higher. If the pretest probability for this 40-year-old female with a breast lump is estimated to be 50% rather than 0.1%, the calculated post-test probability is approximately 95% (see calculation below).
Calculation: